[자바] Two Pointer 알고리즘

Two Pointer 알고리즘 (투 포인터 알고리즘)

개념

• 투 포인터 알고리즘은 배열이나 리스트에서 두 개의 포인터를 사용하여 효율적으로 목표(문제)를 해결하는 기법으로 정렬된 배열에서 특정 조건을 만족하는 부분을 찾을 때 사용하면 시간 복잡도를 줄이는 매우 좋다.

로직

• 두 개의 포인터를 사용하여 배열을 탐색
• 보통 하나를 왼쪽(배열 인덱스0)에서 시작, 다른 하나는  오른쪽에서 시작하여  특정 조건을 만족하는 경우를 찾는다.

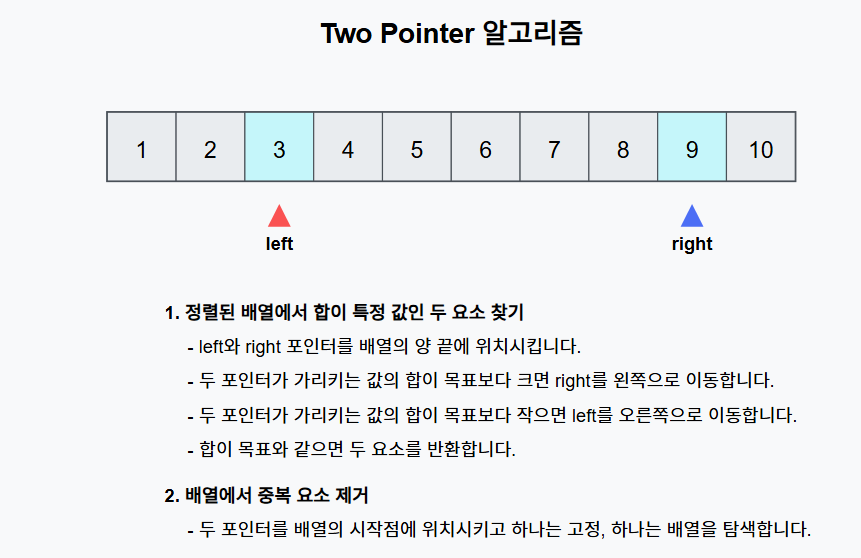
문제 유형에따라 오른쪽 시작 지점이 0부터 시작할 수도 있고 배열 인덱스의 최대치에서부터 시작할 수 있다.

---

대표 유형

두 수 의 합

• 배열이 정렬된 상태에서 투 포인터를 사용하여 두 수의 합이 특정 값이 되는지 찾는 문제

로직

1. 왼쪽 인덱스 left를 0으로, 오른쪽 인덱스 right를 배열의 끝으로 설정합니다.
2. 두 수의 합이 목푯값보다 작으면 left를 증가시키고, 크면 right를 감소시킵니다.
3. 합이 목표값과 같으면 true를 반환합니다.

코드

import java.util.Arrays;

public class TwoPointerSum {
    public static boolean twoSum(int[] arr, int target) {
        Arrays.sort(arr); // 정렬된 배열을 가정
        int left = 0, right = arr.length - 1;

        while (left < right) {
            int sum = arr[left] + arr[right];
            if (sum == target) {
                return true; // 합이 target과 같으면 true
            } else if (sum < target) {
                left++; // 합이 작으면 left 증가
            } else {
                right--; // 합이 크면 right 감소
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 4, 7, 11, 15};
        int target = 9;
        System.out.println(twoSum(arr, target)); // true (4 + 5)
    }
}

---

연속된 부분 수열

•  투 포인터를 활용하여 연속된 부분 배열의 합이 특정 값을 만족하는 경우를 찾는 문제

로직

1. left를 0으로 설정합니다.
2. right를 0부터 시작하여 하나하나 더해가면서 합을 구합니다.
3. 만약 목표값보다목푯값보다 더한 값이 커지면, left값을 하나씩 빼며 목푯값보다 작아지도록 합을 줄여 나갑니다.

코드

public class TwoPointerSubarraySum {
    public static boolean subarraySum(int[] arr, int target) {
        int left = 0, sum = 0;

        for (int right = 0; right < arr.length; right++) {
            sum += arr[right]; // 현재 원소 추가

            while (sum > target) { // 목표값보다 크면 left 증가
                sum -= arr[left++];
            }

            if (sum == target) {
                return true; // 목표값을 만족하는 부분 배열 존재
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[] arr = {1, 3, 2, 5, 7, 2};
        int target = 10;
        System.out.println(subarraySum(arr, target)); // true (3 + 2 + 5)
    }
}

---

가장 긴 부분 수열

• 연속된 부분 배열 중 특정 조건을 만족하는 가장 긴 부분 수열의 길이를 찾는 문제

로직

1. left를 0으로 설정하고, sum을 0으로 초기화합니다.
2. right를 0부터 시작하여 합을 더해가면서 목푯값보다 커지면 left를 증가시켜 목푯값보다 작아지도록 합을 줄입니다.
3. right가 더해지거나 left가 값이 빠질 때마다 계속해서 현재 길이를 갱신한다 이때 길이를 갱신하는 방법은
4.  maxLength = (현재전까지의 가장 긴 값, (right - left +1)) => 비교하여 가장 긴 값을 경신한다.

코드

public class LongestSubarray {
    public static int longestSubarray(int[] arr, int limit) {
        int left = 0, maxLength = 0, sum = 0;

        for (int right = 0; right < arr.length; right++) {
            sum += arr[right]; // 현재 원소 추가

            while (sum > limit) { // 조건을 만족하지 않으면 left 증가
                sum -= arr[left++];
            }

            maxLength = Math.max(maxLength, right - left + 1); // 최대 길이 갱신
        }
        return maxLength;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5};
        int limit = 7;
        System.out.println(longestSubarray(arr, limit)); // 3 (1+2+3 or 2+3+2)
    }
}