백준11403 경로찾기 파이썬 풀이

https://www.acmicpc.net/problem/11403

11403번: 경로 찾기

가중치 없는 그래프가 주어질때 모든 정점 에 대해서 모든 정점으로 가는 길이 존재 하는 없는 지 구하는 문제로
플로이드 워셜 알고리즘을 사용했다 
플로이드 워셜 알고리즘은 모든 정점에서 모든 정점으로 가는 최소 거리를 구할수 있게 해주는 알고리즘이다
 
입력
첫줄에 정점의 갯수 n
두번째 줄부터 n개 줄까지 서로 각 정점 i 에서 j로 가는 길을 있다면 1 없다면 0으로  주어진다
 
출력 
i에서 j로 가는 길이 있다면 1 없다면 0으로 출력해야한다 

이 예제로 예를 들면

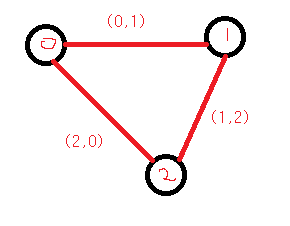
위의 주어진 입력을 표현 하게 되면 이렇게 된다. 
 
플로이드 워셜 그대로 사용한 코드

import sys
input = sys.stdin.readline
n=int(input())
max=10000000
graph=[[max]*(n) for _ in range(n)]

for i in range(n):
    array=list(map(int,input().split()))
    for k in range(n):
        if array[k]==1:
            graph[i][k]=1
for k in range(n):
    for a in range(n):
        for b in range(n):
            graph[a][b]=min(graph[a][b],graph[a][k]+graph[k][b])
for a in range(n):
    for b in range(n):
        if graph[a][b]==max:
            print(0,end=" ")
        else:
            print(1,end=" ")
    print()

 
플로이드 워셜 이용한 코드

import sys
input = sys.stdin.readline
n=int(input())
graph=[list(map(int,input().split())) for _ in range(n)]

for k in range(n):
    for i in range(n):
        for j in range(n):
            if graph[i][k] and graph[k][j]:
                graph[i][j]=1

for i in range(n):
    for j in range(n):
        print(graph[i][j],end=' ')
    print()